SpaceX
浅尝编译原理
编辑
2024-03-23
服务端
0
请注意，本文编写于 208 天前，最后修改于 77 天前，其中某些信息可能已经过时。

目录

为什么你要学习编译原理？
理解代码：编译器的前端技术
词法分析/Lexical Analysis
语法分析/Syntactic Analysis
语义分析/Semantic Analysis
总结
正则文法和有限自动机
语法分析
递归下降
上下文无关文法
左递归下降无限循环问题
确保正确的优先级
确保正确的结合性
消除左递归

为什么你要学习编译原理？

编译原理深入编程语言的结构、语法、语义和复杂的算法，涉及计算机体系结构、操作系统和编程语言之间的交互，还包括存储器管理、进程调度和并发控制等关键概念。通过编译原理的学习，我们知道如何将高级语言转换为底层的机器语言或中间代码，从而理解程序的执行过程及其背后的原理，进而了解如何优化和转换程序代码，程序的抽象思维能力对于解决各种计算机科学问题和设计复杂系统也是非常有帮助的；另一发面，这也有助于我们开发语言处理工具，如编译器、解释器、静态分析工具等。

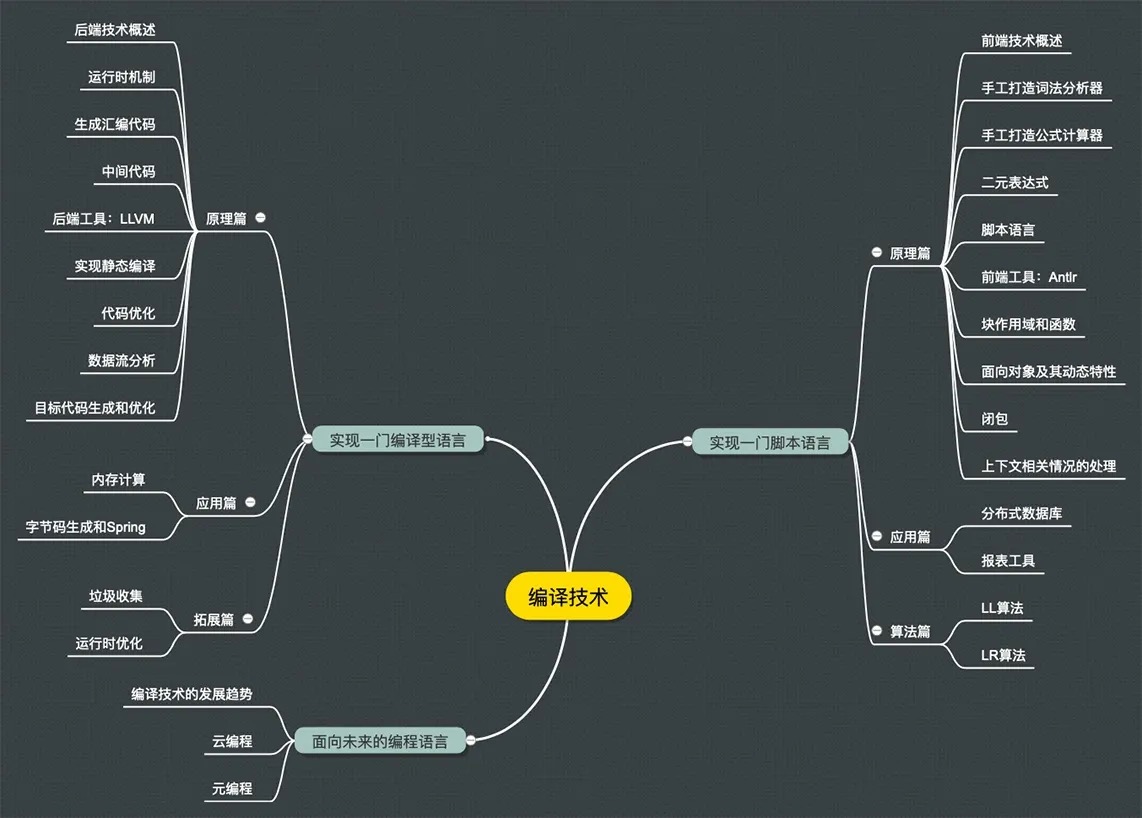
理解代码：编译器的前端技术

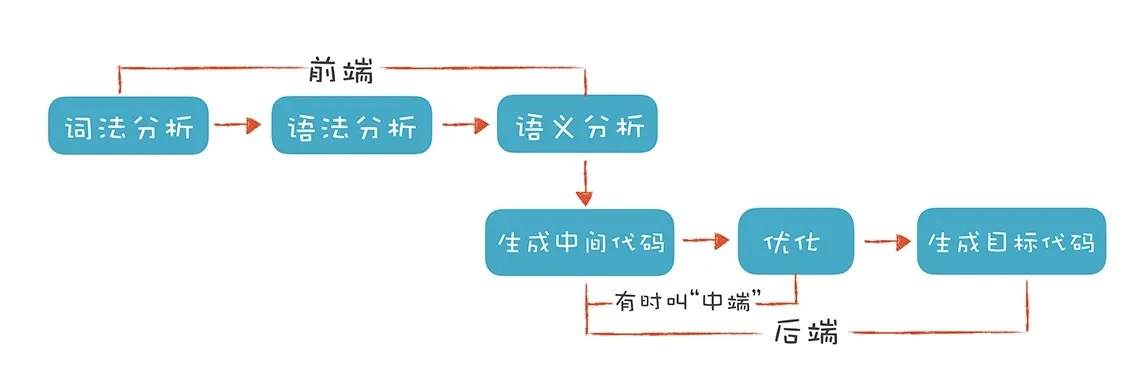
词法分析/Lexical Analysis

一般来说，编译器的第一步称为词法分析。类似于阅读一篇文章，文章是由一个个中文词汇构成的。程序处理也类似，不过在这里这些词汇被称为词法记号，或Token。我们还可以使用词法分析器生成工具来完成这项任务，如Lex（或其GNU版本Flex）。这些工具基于特定规则工作，这些规则通过正则文法表达，符合正则文法的表达式被称为正则表达式。生成工具会读取正则表达式，并生成一种称为有限自动机的算法，以执行具体的词法分析。

正则文法是一种非常常见的规则体系，实际上，当你编写正则表达式时，你就在使用正则文法。

词法分析是编译器的一个关键步骤，它将源代码转化为一系列的词法记号，这些记号是语法分析的基础。词法分析器不仅需要识别有效的词法记号，还需要处理错误和异常情况。现代编译器通常会结合词法分析和语法分析，以提高处理效率和准确性。此外，词法分析器的性能对编译器的整体性能有重要影响，因此优化词法分析器是编译器设计中的一个重要课题。

语法分析/Syntactic Analysis

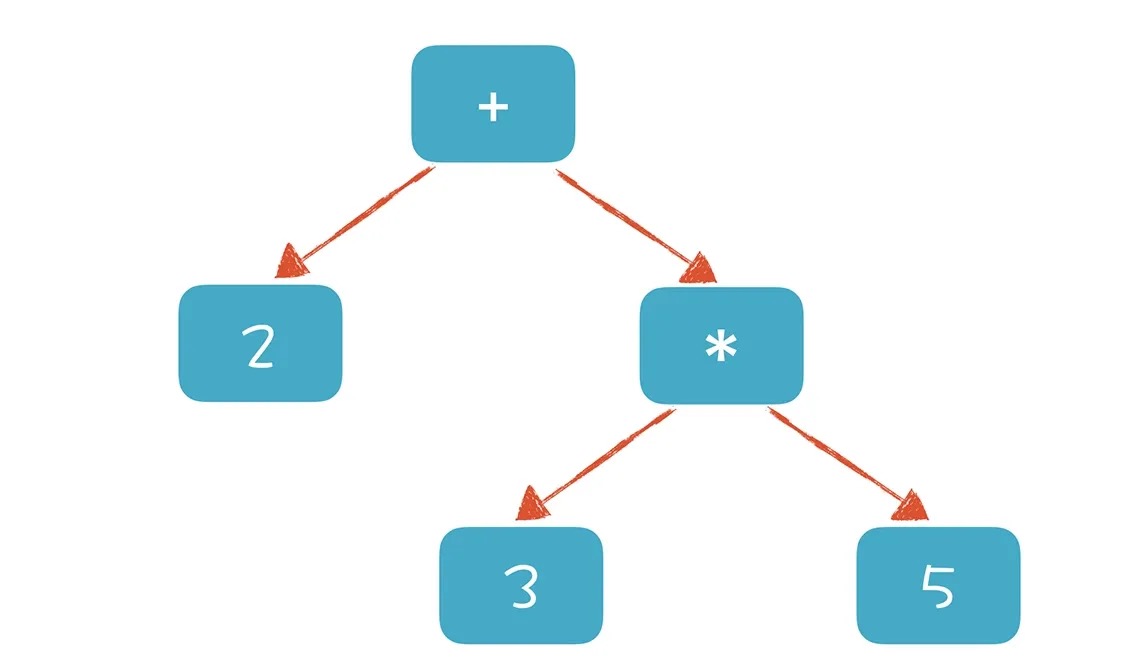
程序同样具备明确的语法结构，语法分析的过程实际上就是构建一棵树。这棵树被称为抽象语法树（Abstract Syntax Tree，AST）。在这棵树中，每个节点（或子树）代表一个语法单元，这些单元的构成规则即为语法。每个节点还可以包含更低级的节点。

构建AST之后，计算机处理程序变得更加容易。例如，对于表达式构成的这棵树，通过遍历根节点及其子节点，可以轻松计算出表达式的值。

AST不仅在计算表达式值时有用，还在代码优化、代码生成和静态分析等方面发挥重要作用。AST去除了源代码中的冗余信息，仅保留了必要的语法和语义信息，使得后续处理更加高效。语法分析器利用预定义的语法规则将源代码解析为AST，这一过程称为解析（Parsing）。语法分析器通常分为自顶向下解析器和自底向上解析器，前者从根节点开始逐步展开，而后者从叶节点开始逐步归约为根节点。

你已经有了一定的经验，可以尝试寻找现成的工具来帮助你构建和处理AST。例如，Yacc（或其GNU版本Bison）、Antlr、JavaCC等都是常用的语法分析器生成工具。这些工具基于语法规则生成解析器，能够自动化地将源代码转换为AST，从而简化开发过程。

此外，AST在静态代码分析工具中也得到了广泛应用，这些工具通过分析AST来检测代码中的潜在问题，如语法错误、代码风格问题和安全漏洞。AST的结构化特性使其在代码转换和重构工具中也得到了广泛应用。

语义分析/Semantic Analysis

语义分析的目的是让计算机准确理解我们的意图，消除任何模棱两可的地方。实际上，语义分析并没有想象中那么复杂，因为计算机语言的语义通常可以通过一系列规则来表达，只需检查代码是否符合这些规则即可。例如： 语义分析的任务

  • 数据类型检查：确定某个表达式的计算结果是什么数据类型。如果存在数据类型不匹配的情况，需要决定是否进行自动类型转换。
  • 变量作用域解析：在代码块的内部和外部有相同名称的变量时，确定在执行时到底使用哪个变量。这类似于在句子“我喜欢又聪明又勇敢的你”中明确“你”指的是谁。
  • 唯一性检查：在同一作用域内，不允许存在两个名称相同的变量。例如，不能在声明一个变量a后，紧接着又声明一个同名的变量a。
  • 函数调用检查：验证函数调用时传递的参数是否与函数定义匹配，包括参数的数量和类型。
  • 控制流分析：确保程序中的控制流逻辑正确，如检查循环和条件语句的正确性，防止无限循环和死代码。
  • 变量初始化检查：确保在使用变量之前已经对其进行了初始化，防止未初始化变量的使用导致运行时错误。
  • 类型推断：在某些编程语言中，编译器可以通过语义分析自动推断变量的类型，从而简化代码编写。

总结

  • 词法分析：
    • 定义：将程序分割成一个个Token的过程。
    • 实现：可以通过构造有限自动机来实现。
    • 工具：常用工具如Lex（或其GNU版本Flex）基于正则表达式生成词法分析器。
  • 语法分析：
    • 定义：识别程序的结构，并形成一棵便于计算机处理的抽象语法树（AST）。
    • 实现：可以使用递归下降算法或其他解析算法来实现。
    • 工具：常用工具如Yacc（或其GNU版本Bison）、Antlr、JavaCC等生成语法分析器。
  • 语义分析：
    • 定义：消除语义上的模糊，生成一些属性信息，使计算机能够依据这些信息生成目标代码。
    • 任务：包括数据类型检查、变量作用域解析、唯一性检查等。
    • 工具：语义分析器通常构建符号表，用于存储变量、函数、类等符号的信息。

通过词法分析、语法分析和语义分析，编译器能够将源代码转换为结构化的中间表示，并最终生成高效的目标代码。这些步骤共同确保了程序的正确性和高效性。

正则文法和有限自动机

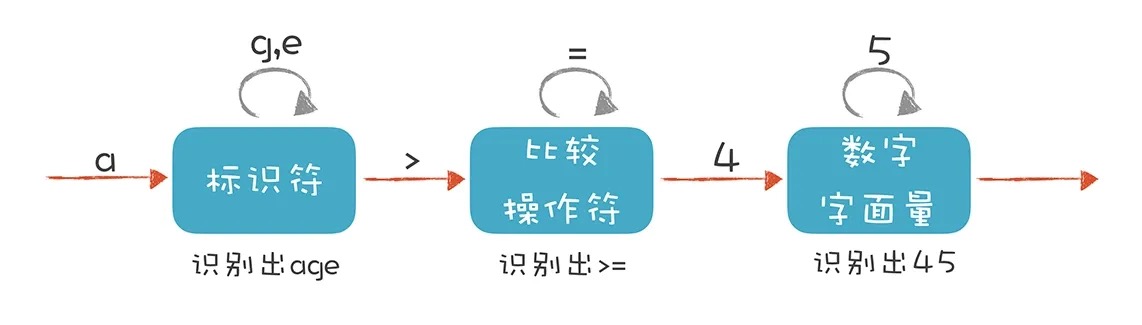
通过解析 age >= 45，我们来描述一下标识符、比较操作符和数字字面量这三种Token的词法规则。

  • 标识符：第一个字符必须是字母，后面的字符可以是字母或数字。
  • 比较操作符：> 和 >=（其他比较操作符暂时忽略）。
  • 数字字面量：全部由数字构成（像带小数点的浮点数，暂时不管它）。

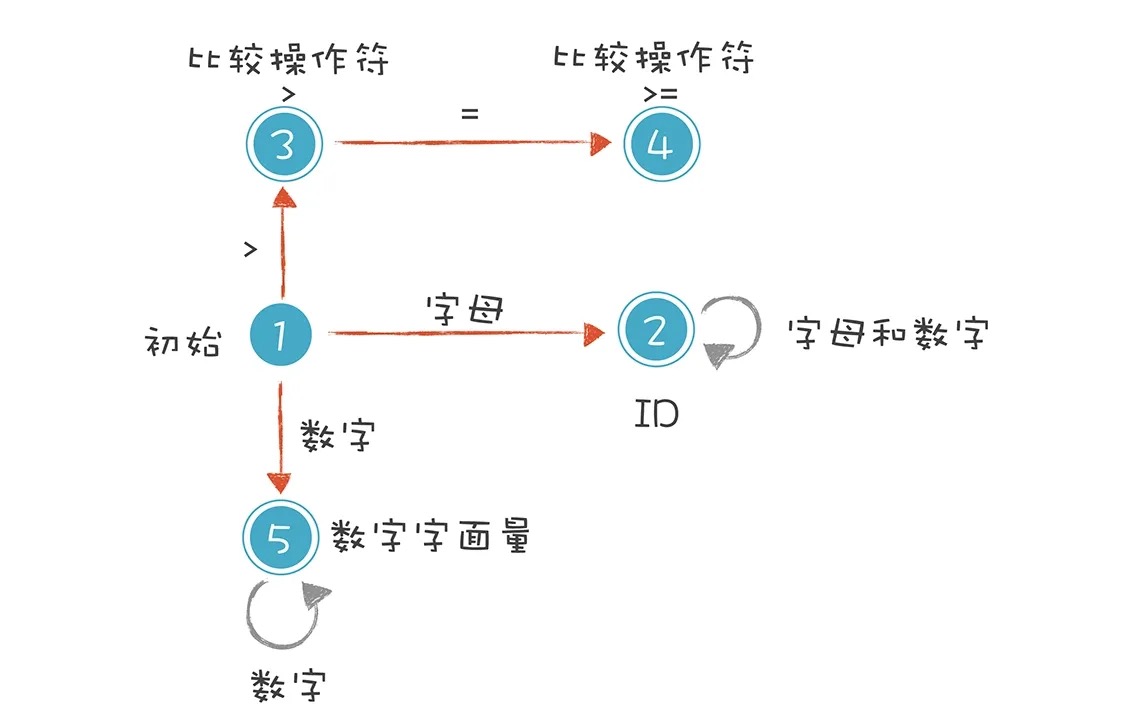
上面的例子涉及了4种Token，这4种Token用正则表达式表达，是下面的样子：

powershell
Id :        [a-zA-Z_] ([a-zA-Z_] | [0-9])*
IntLiteral: [0-9]+
GT :        '>'
GE :        '>='

语法分析

递归下降

递归下降解析（Recursive Descent Parsing）是一种用于语法分析的技术，最终生成抽象语法树（AST）。在语法分析中，算法可以分为自顶向下和自底向上两类。递归下降解析是一种常见的自顶向下算法，它通过遍历抽象语法树来解析输入的语句。

递归下降解析算法的工作原理类似于编写一组递归函数，每个函数对应一个语法规则。解析器通过调用这些函数来分析输入的语句，并构建抽象语法树。递归下降解析的优点在于其实现简单、易于理解和调试。然而，它也有一些限制，例如难以处理左递归的语法规则。

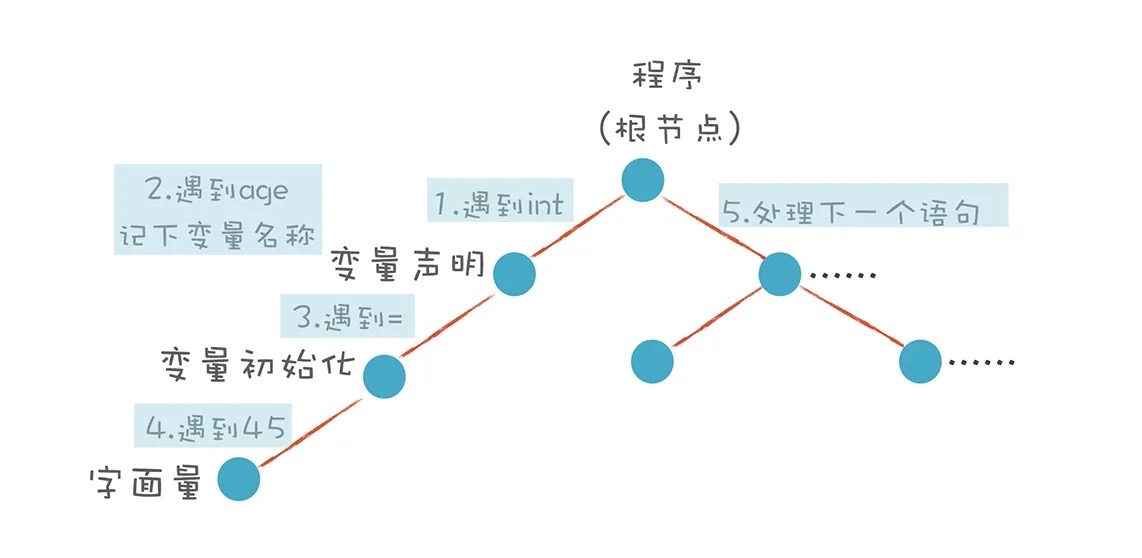
我们先来用形式化的方法表示变量声明语句的规则。首先，左边是一个非终结符（Non-terminal），而右边是它的产生式（Production Rule）。在语法解析中，左边的非终结符会被右边的产生式替代。如果替代后仍然存在非终结符，那么这个替代过程会继续进行，直到所有非终结符都被终结符（Terminal）替代，也就是具体的词法单元（Token）。只有终结符才能构成抽象语法树（AST）的叶子节点。这个过程被称为推导（Derivation）过程。

powershell
<变量声明> ::= <类型> <标识符> ";"
<类型> ::= "int" | "float" | "char"
<标识符> ::= <字母> | <字母><标识符>
<字母> ::= "a" | "b" | ... | "z" | "A" | "B" | ... | "Z"

我们可以将解析变量声明语句和表达式的算法分别写成函数。在语法分析过程中，这些函数将与后续的Token串进行模式匹配。如果匹配成功，则返回一个AST节点；如果匹配失败，则返回null。如果在解析过程中发现与语法规则不符，则报告编译错误。

在这个过程中，上级文法嵌套下级文法，上级的算法调用下级的算法，表现在生成 AST 中，上级算法生成上级节点，下级算法生成下级节点，这就是“下降”的含义。程序结构基本上是跟文法规则同构的。这就是递归下降算法的优点

powershell
// AST
Programm Calculator
    IntDeclaration age
        AssignmentExp =
            IntLiteral 45

用代码解析Int申明的代码如下：

objectivec
fn int_declare<T: TokenReader>(&self, tokens: &mut T) -> Result<Option<SimpleASTNode>, io::Error> {
    let token = tokens.peek();
    if token.is_none() || token.unwrap().get_type() != TokenType::Int {
        return Ok(None);
    }

    //  token.Type = TokenType::Int

    let _ = tokens.read(); // 消耗掉int
    let e = io::Error::new(io::ErrorKind::InvalidInput, "variable name expected");
    let token = tokens.peek().ok_or(e)?;

    if token.get_type() != TokenType::Identifier {
        let e = io::Error::new(io::ErrorKind::InvalidInput, "variable name expected");
        return Err(e);
    }

    // token.Type = TokenType::Identifier

    let token = tokens.read().unwrap(); // 消耗掉 Identifier
    // 创建当前节点，并把变量名记到AST节点的文本值中，这里新建一个变量子节点也是可以的
    let mut node = SimpleASTNode::new(ASTNodeType::IntDeclaration, token.get_text());

    let token = tokens.peek();
    if !token.is_none() && token.unwrap().get_type() == TokenType::Assignment {
        let _ = tokens.read(); // 消耗掉 =

        let e = io::Error::new(io::ErrorKind::InvalidInput,
                               "invalid variable initialization, expecting an expression");
        let child = self.additive(tokens)?.ok_or(e)?;
        node.add_child(RefCell::new(Rc::new(child)));
    }

    let token = tokens.peek();
    if token.is_none() || token.unwrap().get_type() != TokenType::SemiColon {
        let e = io::Error::new(io::ErrorKind::InvalidInput, "invalid statement, expecting semicolon");
        return Err(e);
    }

    let _ = tokens.read(); // 消耗掉 ;


    Ok(Some(node))
    }

上下文无关文法

上下文无关文法（Context-Free Grammar, 简称CFG）可以用来描述算术表达式，并且可以通过分级规则来确保乘法优先于加法。我们将规则分成两级：第一级是加法规则，第二级是乘法规则。乘法规则作为加法规则的子规则，这样在生成AST时，乘法节点会成为加法节点的子节点，从而优先计算。

为了更好地理解和应用这些规则，我们可以用Antlr工具的写法来表示这些语法规则。下面是用BNF（巴科斯范式）和Antlr工具的写法来表示加法和乘法规则的示例：

BNF表示法 在BNF中，我们可以用以下规则来表示加法和乘法：

powershell
A -> M | A + M
M -> int | M * int

或者拆成更简单的形式：

powershell
A -> M
A -> A + M
M -> int
M -> M * int

Antlr表示法 在Antlr中，我们可以用类似的语法规则来表示：

powershell
grammar Arithmetic;

expression : additiveExpression;

additiveExpression
    : multiplicativeExpression
    | additiveExpression '+' multiplicativeExpression
    ;

multiplicativeExpression
    : INT
    | multiplicativeExpression '*' INT
    ;

INT : [0-9]+ ;
WS : [ \t\r\n]+ -> skip;

应该注意的是，加法规则中还递归地又引用了加法规则。通过这种递归的定义，我们能展开、形成所有各种可能的算术表达式。比如2+3*5的推导过程：

powershell
-->additiveExpression + multiplicativeExpression
-->multiplicativeExpression + multiplicativeExpression
-->IntLiteral + multiplicativeExpression
-->IntLiteral + multiplicativeExpression * IntLiteral 
-->IntLiteral + IntLiteral * IntLiteral

这种文法已经没有办法改写成正则文法了，它比正则文法的表达能力更强，叫做上下文无关文法。正则文法是上下文无关文法的一个子集。上下文无关文法的强大表达能力，可以处理递归结构和嵌套的语法规则。正是因为上下文无关文法允许递归调用，因此它能够描述和解析更复杂的语言结构，而这是正则文法无法做到的。 正则文法 正则文法是一种限制更严格的文法，它的产生式规则形式如下：

powershell
A -> aB | a

这里，A 和 B 是非终结符，a 是终结符。正则文法的特点是右边的产生式只能有一个非终结符，并且这个非终结符必须出现在最右边（右线性文法）或最左边（左线性文法）。正则文法不能表达递归结构，因此它的表达能力有限。 上下文无关文法 上下文无关文法允许产生式的右边包含任意数量和顺序的终结符和非终结符。它的产生式规则形式如下：

powershell
A -> α

这里，A 是非终结符，α 可以是包含终结符和非终结符的任意字符串。上下文无关文法允许递归调用，因此可以表达更复杂的语法结构，比如嵌套的括号、嵌套的表达式等。

左递归下降无限循环问题

为了简单化，我们采用下面这个简化的文法，去掉了乘法的层次：

powershell
additiveExpression
    :   IntLiteral
    |   additiveExpression Plus IntLiteral
    ;

在解析 2+3 这样一个最简单的加法表达式的时候，我们直观地将其翻译成算法，结果出现了如下的情况：

  • 首先匹配是不是整型字面量，发现不是；
  • 然后匹配是不是加法表达式，这里是递归调用；
  • 会重复上面两步，无穷无尽。

左递归是递归下降算法无法处理的主要问题，因为它会导致无限递归。我们需要将左递归转换为右递归，以便递归下降解析器能够正确处理。

就这个推导说说我目前的理解，其中最开始不能理解的根本原因就是没能理解语法规则之间的相互关系，以及与此相关的token的消耗。比如，例子 A->Int | A + Int，在最开始的理解中，错误以为这两条是顺序关系，想当然认为token的消耗是像字符串匹配一样“一个接一个”的进行。这种错误思路是这样的：2+3， 首先看token 2， 它是int所以消耗掉，然后类推。而实际上，这两条规则是从某种程度上是“互斥”的关系。也就是说，2+3 要么是 Int， 要么是 A+Int，在没有找到合适的规则前，token 是不会被消耗的。由此，在深度优先实现中，就有老师所说的推导实现过程。总的要解决的问题是，2+3 是不是 A，能不能用这条 A 规则来解释。那么就看它是否满足 A 的具体规则。首先，2+3 显然不是 Int，因此没有 token 消耗。然后，在匹配 A + Int 时，上来就要看 2+3 是不是 A，不断要解决原来的问题，从而就产生了所谓左递归。所以在深度优先情况下，打破无穷递归，就把规则改为A-> Int | Int + A。这时，推导， 2+3 显然不是Int。于是看 Int + A。2 显然是Int，于是消耗掉；再看 +，消耗掉；再看 3 是不是 A，3 显然是 Int，所以返回。

怎么解决？

powershell
additiveExpression
    :   multiplicativeExpression
    |   additiveExpression Plus multiplicativeExpression
    ;

multiplicativeExpression
    :   IntLiteral
    |   IntLiteral Star multiplicativeExpression
    ;

现在我们貌似解决了左递归问题，运行这个算法解析 2+3*5，得到下面的 AST：

powershell
Programm Calculator
    AdditiveExp +
        IntLiteral 2
        MulticativeExp *
            IntLiteral 3
            IntLiteral 5

是不是看上去一切正常？可如果让这个程序解析2+3+4呢？

powershell
Programm Calculator
    AdditiveExp +
        IntLiteral 2
        AdditiveExp +
            IntLiteral 3
            IntLiteral 4

可以看到，这里的计算顺序发生错误了，连续相加的表达式要从左向右计算，这是加法运算的结合性规则。但按照我们生成的 AST，变成从右向左了，先计算了3+4，然后才跟2相加，这样很明显是有问题的。

  • 首先调用乘法表达式匹配函数 multiplicative()，返回了一个字面量节点 2
  • 接着看看右边是否能递归地匹配加法表达式
  • 匹配的结果，真的返回了一个加法表达式3+4，这个变成了第二个子节点。错误就出在这里了，这样的匹配顺序，3+4一定会成为子节点，在求值时被优先计算

总结：递归算法是很好的自顶向下解决问题的方法，体现了分治（Divide and Conquer）的思想，即将一个大问题分解为若干个小问题来解决，是计算机领域的一个核心的思维方式。分治思想在许多经典算法中得到了广泛应用，例如快速排序、归并排序和二叉树遍历等。

通过上文，我们已经知道语法规则是由上下文无关文法表示的，而上下文无关文法是由一组替换规则（又叫产生式）组成的，比如算术表达式的文法规则可以表达成下面这种形式：

add ::= mul | add + mul
mul ::= pri | mul * pri
pri ::= Id | Num | (add)

这种写法叫做巴科斯范式，简称BNF。

确保正确的优先级

我们由加法规则推导到乘法规则，这种方式保证了 AST 中的乘法节点一定会在加法节点的下层，也就保证了乘法计算优先于加法计算。

powershell
exp -> or | or = exp   
or -> and | or || and
and -> equal | and && equal
equal -> rel | equal == rel | equal != rel
rel -> add | rel > add | rel < add | rel >= add | rel <= add
add -> mul | add + mul | add - mul 
mul -> pri | mul * pri | mul / pri 
pri -> Id | Literal | (exp)

这里表达的优先级从低到高是：赋值运算、逻辑运算（or）、逻辑运算（and）、相等比较（equal）、大小比较（rel）、加法运算（add）、乘法运算（mul）和基础表达式（pri）。

确保正确的结合性

前面的内容中，针对算术表达式写的第二个文法是错的，因为它的计算顺序是错的。2+3+4这个算术表达式，先计算了3+4然后才和2相加，计算顺序从右到左，正确的应该是从左往右才对。

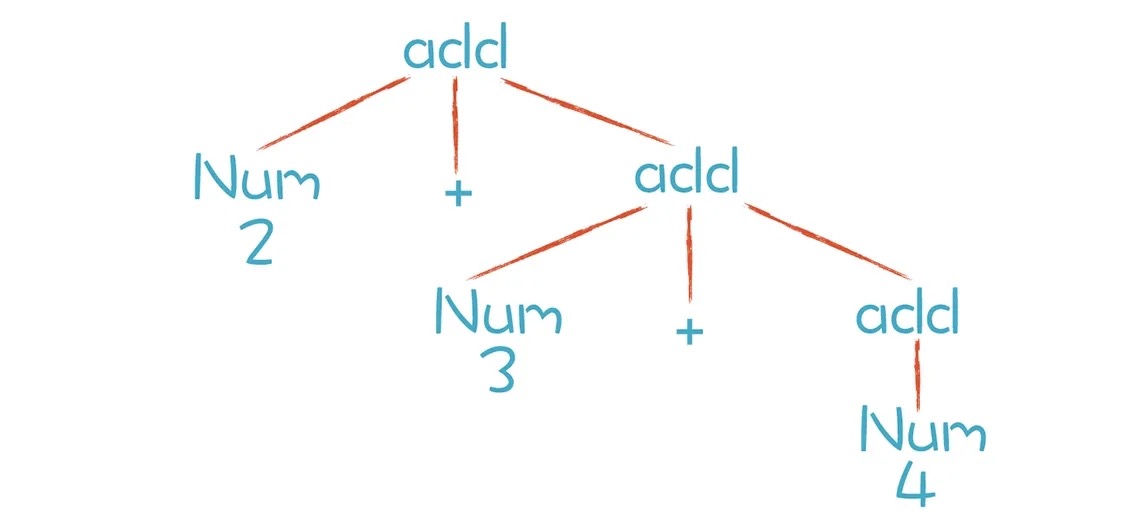
根据这个 AST 做计算会出现计算顺序的错误。不过如果我们将递归项写在左边，就不会出现这种结合性的错误。于是我们得出一个规律：对于左结合的运算符，递归项要放在左边；而右结合的运算符，递归项放在右边。

所以你能看到，我们在写加法表达式的规则的时候，是这样写的：

add -> mul | add + mul

这样写是有左递归问题。那我们如何解决左递归问题呢？

消除左递归

消除左递归，用一个标准的方法，就能够把左递归文法改写成非左递归的文法。以加法表达式规则为例，原来的文法是add -> add + mul，现在我们改写成：

powershell
add -> mul add'
add' -> + mul add' | ε

代码中，ε（epsilon）是空集的意思。接下来，我们用刚刚改写的规则再次推导一下2+3+4这个表达式，得到了下图中左边的结果：

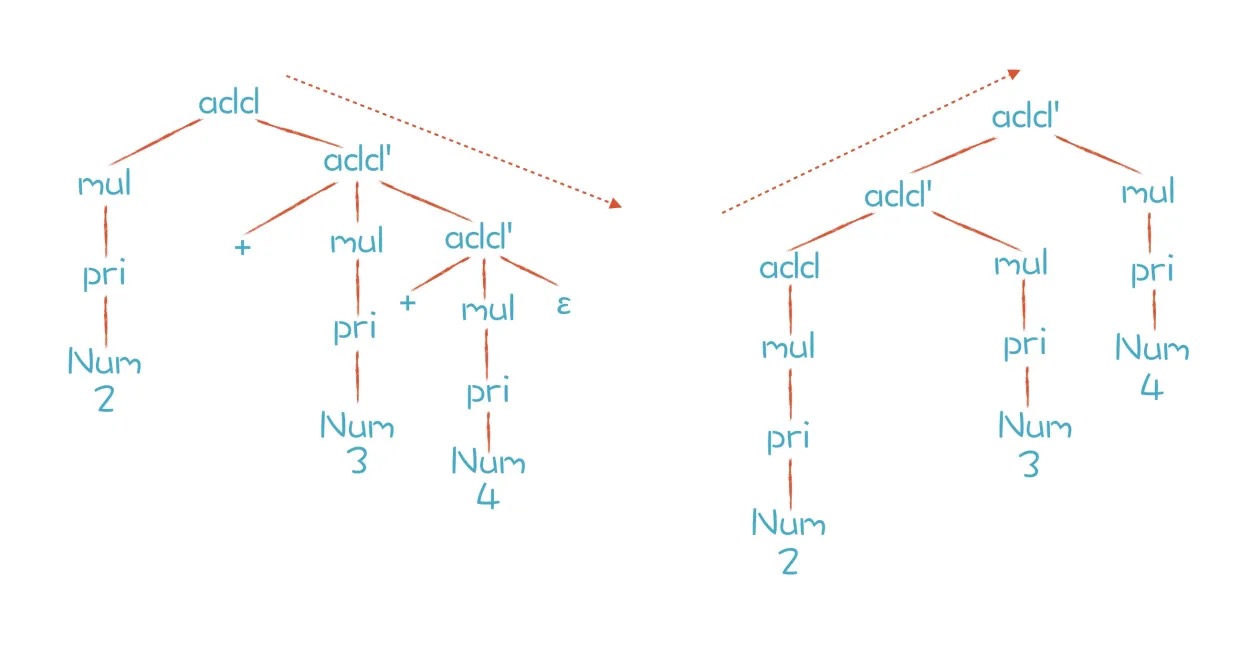
左边的分析树是推导后的结果。问题是，由于 add’的规则是右递归的，如果用标准的递归下降算法，我们会跟上一讲一样，又会出现运算符结合性的错误。我们期待的 AST 是右边的那棵，它的结合性才是正确的。那么有没有解决办法呢？ 如果用EBNF方式表达，也就是允许用*号和+号表示重复，上面两条规则可以合并成一条：

powershell
add -> mul (+ mul)* 

// 伪代码
mul();
while(next token is +){
  mul()
  createAddNode
}

我们扩展一下话题。在研究递归函数的时候，有一个概念叫做尾递归，尾递归函数的最后一句是递归地调用自身。

编译程序通常都会把尾递归转化为一个循环语句，使用的原理跟上面的伪代码是一样的，这也是一种编译优化技术。编译器可以将尾递归转换为循环避免了递归调用的栈开销。这种优化称为尾递归优化（Tail Call Optimization, TCO）。通过将尾递归转换为循环，编译器可以重复使用同一个栈帧，从而大大减少内存消耗和函数调用的开销。

尾递归是指在函数的最后一步调用自身的递归函数。在尾递归调用中，递归调用是函数的最后一个操作，之后没有其他操作需要执行。

python
// 普通递归
func factorial(n int) int {
    if n == 0 {
        return 1
    }
    return n * factorial(n-1)
}

# Example usage
    fmt.Println(factorial(5)) // 输出: 120

// 
func factorialTailRecursive(n int, acc int) int {
    if n == 0 {
        return acc
    }
    return factorialTailRecursive(n-1, n*acc)
}

    fmt.Println(factorialTailRecursive(5, 1)) // 输出: 120

本文作者:sora

本文链接:

版权声明:本博客所有文章除特别声明外，均采用 BY-NC-SA 许可协议。转载请注明出处！